通常情况下质谱仪器在每个样本中都能够检测到上百,甚至上千个蛋白或代谢物。在统计模型中,我们认为每个蛋白及代谢物都属于一个变量,那么我们一组样本就等同于拥有了成百上千的变量,但同时对上千的变量进行分析显然是不现实的,不仅耗费算力,而且也很难提取出关键信息。在这种背景下,降维就成为了我们的解决方案。
降维指的是将部分的具有一定关系的变量根据不同的算法融合为一个新的变量,以达到降低维度的效果,之后我们就可以将原本高维的数据投影到低维空间,去掉冗余属性,但同时尽可能地保留高维空间的重要信息和特征。
从具体的降维方法来分类,主要可分为线性和非线性两大类。其中,线性方法的本质是观察坐标系替换的时候,新坐标轴是原始特征的一个线性组合,常用的有主成分分析(Principal Component Analysis,PCA)、多维尺度分析(Multidimensional Scaling, MDS)、非矩阵分解(Multidimensional ScalingNMF)等;相较于线性方法,非线性方法并不会生成一个基于原始特征的线性组合生成新坐标系,通过非线性变换将高维数据投影到低维空间,并保留数据的局部和全局结构,常用的有等距特征映射(Isometric Mapping, ISOMAP)、局部线性嵌套(Locally Linear Embedding, LLE)、T分布随机近邻嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)等。
T-SNE算法是一种用于降维的机器学习算法,它会将数据点之间的相似度转化为一个概率分布,并使降维前后数据各自对应的概率分布尽可能的接近,从而能够在低维空间里保持其在高维空间里所携带的信息(比如高维空间里有的清晰的分布特征,转到低维度时也依然存在)。相较于常见的PCA方法,T-SNE能够更好地突出数据集中的成簇特征,并且更适用于处理复杂的非线性关系,常用于图像识别、生物信息学等领域,t-SNE的主要用途是可视化和探索高维数据。但遗憾的是,T-SNE一般只能应用于图形可视化,不能用于预测测试集样本。与PCA不同,t-SNE可以更好地应用于线性和非线性良好聚类的数据集,并产生更有意义的聚类。尽管t-SNE在可视化分离良好的群集方面非常出色,但大多数情况下它无法保留数据的整体几何形状。
1. 导入数据
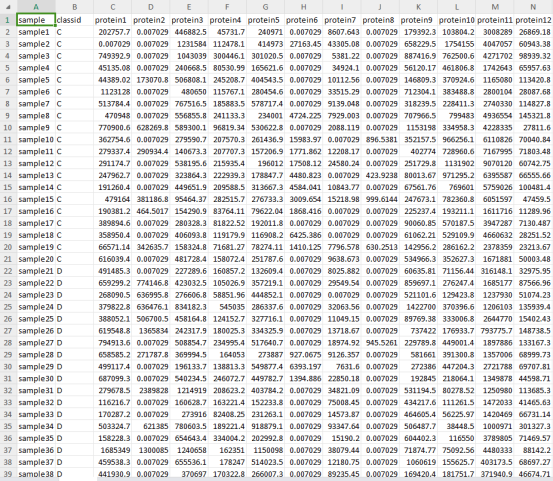
将上述图片中格式的数据导入R中,每一列代表一个蛋白,每一行代表一个样本。
2. T-SNE算法

3. 绘制T-SNE图像


最终得到的T-SNE图像,如图所示
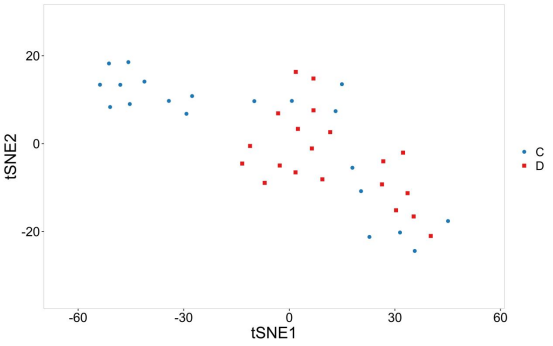
-
 深化合作 | SCIEX全球副总裁蔡俊松一行来访百趣,共探合作新方向近日,SCIEX全球副总裁、中国区总经理蔡俊松先生与中国市场副总监江峥女士莅临上海百趣生物医学科技有限公司(以下简称“百趣生物”)苏州产能中心。此次访问,蔡俊松先生、江峥女士与百趣生物总裁邓军亮先生及市场中心总监程羿淳女士进行了深入的交流。2024-04-16
深化合作 | SCIEX全球副总裁蔡俊松一行来访百趣,共探合作新方向近日,SCIEX全球副总裁、中国区总经理蔡俊松先生与中国市场副总监江峥女士莅临上海百趣生物医学科技有限公司(以下简称“百趣生物”)苏州产能中心。此次访问,蔡俊松先生、江峥女士与百趣生物总裁邓军亮先生及市场中心总监程羿淳女士进行了深入的交流。2024-04-16 -
 薅羊毛 | 组学推荐,豪礼送不停时光荏苒,百趣生物已经迎来了第12个生日!我们始终坚守初心,致力于质谱技术在动植物生命科学和医学健康领域的研究与创新。在这个值得纪念的日子里,我们特别策划了一场“推荐有礼”活动,邀请广大科研小伙伴们共同参与,推荐您身边有组学需求的伙伴,成功签单,即可获得丰厚礼品!2024-03-13
薅羊毛 | 组学推荐,豪礼送不停时光荏苒,百趣生物已经迎来了第12个生日!我们始终坚守初心,致力于质谱技术在动植物生命科学和医学健康领域的研究与创新。在这个值得纪念的日子里,我们特别策划了一场“推荐有礼”活动,邀请广大科研小伙伴们共同参与,推荐您身边有组学需求的伙伴,成功签单,即可获得丰厚礼品!2024-03-13 -
 第37期代谢组学暨多元变量统计分析培训班由上海百趣生物医学科技有限公司、Sartorius Stedim Data Analytics AB(简称Sartorius Stedim)联合主办,上海百趣代谢组学技术研究中心承办的“百趣课堂第37期代谢组学暨多元变量统计分析培训”课程将于2024年04月20日-25日在上海举办。2024-03-13
第37期代谢组学暨多元变量统计分析培训班由上海百趣生物医学科技有限公司、Sartorius Stedim Data Analytics AB(简称Sartorius Stedim)联合主办,上海百趣代谢组学技术研究中心承办的“百趣课堂第37期代谢组学暨多元变量统计分析培训”课程将于2024年04月20日-25日在上海举办。2024-03-13 -
 新品发布 | 全面聚焦,探索一碳代谢新可能一碳代谢通路检测能精准定量生物体叶酸、四氢叶酸等代谢物浓度,为推动妇幼相关疾病研究及LDT转化提供新视角和新可能~2024-03-05
新品发布 | 全面聚焦,探索一碳代谢新可能一碳代谢通路检测能精准定量生物体叶酸、四氢叶酸等代谢物浓度,为推动妇幼相关疾病研究及LDT转化提供新视角和新可能~2024-03-05 -
 新品发布 | 直达CNS, 植需NGM尽管植物代谢组学数据的复杂,但为了解决“多”和“准”的核心需求,小趣特为植物领域工作者推出开工BUFF--植物NGM系列产品。2024-03-01
新品发布 | 直达CNS, 植需NGM尽管植物代谢组学数据的复杂,但为了解决“多”和“准”的核心需求,小趣特为植物领域工作者推出开工BUFF--植物NGM系列产品。2024-03-01 -
 项目文章(IF=27.5) | RIN基因新发现:通过根际分泌物塑造抑菌微生态,提升植物免疫力本研究发现植物发育基因可以通过对植物根系分泌物和微生物组组装的影响来控制微生物组介导的抗病性,从而使植物能够利用微生物组编码的基因和功能。2024-03-01
项目文章(IF=27.5) | RIN基因新发现:通过根际分泌物塑造抑菌微生态,提升植物免疫力本研究发现植物发育基因可以通过对植物根系分泌物和微生物组组装的影响来控制微生物组介导的抗病性,从而使植物能够利用微生物组编码的基因和功能。2024-03-01 -
 Cell | CUHK于君团队最新研究成果,除了幽门螺旋杆菌,还有你不知道的胃癌致病因子?胃癌(Gastric cancer, GC)是全球第五大常见癌症,也是导致癌症死亡的主要原因。幽门螺杆菌(Helicobacter pylori, H. pylori)是胃癌的主要危险因素,被列为I型致癌物。2024-02-05
Cell | CUHK于君团队最新研究成果,除了幽门螺旋杆菌,还有你不知道的胃癌致病因子?胃癌(Gastric cancer, GC)是全球第五大常见癌症,也是导致癌症死亡的主要原因。幽门螺杆菌(Helicobacter pylori, H. pylori)是胃癌的主要危险因素,被列为I型致癌物。2024-02-05 -
 百趣生物院士专家工作站——邓春晖教授签约仪式顺利举行2024年1月18日,上海百趣生物院士专家工作站一邓春晖教授签约仪式在上海百趣生物医学科技有限公司(以下简称百趣生物)总部顺利举行。复旦大学邓春晖教授、百趣生物CEO邓军亮等出席签约仪式。2024-01-22
百趣生物院士专家工作站——邓春晖教授签约仪式顺利举行2024年1月18日,上海百趣生物院士专家工作站一邓春晖教授签约仪式在上海百趣生物医学科技有限公司(以下简称百趣生物)总部顺利举行。复旦大学邓春晖教授、百趣生物CEO邓军亮等出席签约仪式。2024-01-22 -
 项目文章 | 蛋白质组学:看蚕豆-小麦间作系统如何击败尖孢镰刀菌与苯甲酸的威胁蚕豆(Vicia faba L.)是中国西南地区最重要的豆科作物之一。但长期单作,会导致蚕豆枯萎病发病率升高,产量和品质下降。已有研究表明,蚕豆与小麦间作可有效缓解蚕豆的自毒作用,抑制蚕豆枯萎病的发生。2024-01-18
项目文章 | 蛋白质组学:看蚕豆-小麦间作系统如何击败尖孢镰刀菌与苯甲酸的威胁蚕豆(Vicia faba L.)是中国西南地区最重要的豆科作物之一。但长期单作,会导致蚕豆枯萎病发病率升高,产量和品质下降。已有研究表明,蚕豆与小麦间作可有效缓解蚕豆的自毒作用,抑制蚕豆枯萎病的发生。2024-01-18 -
 百趣助力乳腺癌亚型新解析,开启乳腺癌治疗新篇章!百趣提供技术服务:非靶标代谢组+脂质组学2023-11-21
百趣助力乳腺癌亚型新解析,开启乳腺癌治疗新篇章!百趣提供技术服务:非靶标代谢组+脂质组学2023-11-21








